Maxwell's equations for the electromagnetic field
[ in units with 
] are:
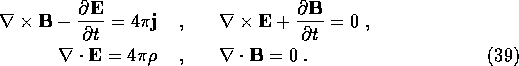
Defining the anti- symmetric tensor 
with
components:
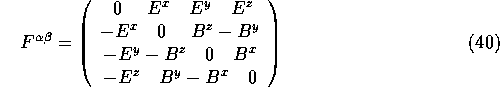
the electric and magnetic fields are given by
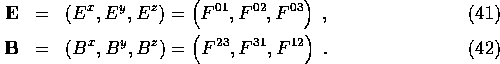
If we also define a current four- vector :
Maxwell's equations can be written as [ Assignment 4 ]
where 
. We have now expressed Maxwell's equations
in tensor form as required by Special Relativity.
The first of these equations implies charge conservaton
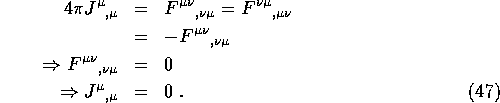
By performing a Lorentz transformation to a frame moving with speed v in the x direction, one can calculate how the electric and magnetic fields change:
We find [ Assignment 4 ] that 
is unchanged, while
where 
and 
is the electric
field parallel and perpendicular to 
. Thus
and 
get mixed.
The four- force on a particle of charge q and velocity
in an electromagnetic field is [ Assignment 4 ]:
The spatial part of 
is the Lorentz force and the time part is the rate of work by this force.
By writing 
, Maxwell's equations give [ Assignment 4 ]:
where
This is the energy momentum tensor of the electromagnetic field.
Note that 
is symmetric as required and the energy
density is [ Assignment 4 ]
